About the project

The challenge

Although the micropolar theory is well established and mathematically mature, reliable procedures for determining micropolar material parameters are still lacking. Even the simplest isotropic micropolar solid requires six independent material constants, yet no universally accepted methodology exists for identifying them. This gap significantly limits the practical application of the theory in engineering simulations.

What has been achieved in our previous research?

Within our earlier CSF scientific project “Fixed-Pole Concept in Numerical Modelling of Cosserat Continuum” (FIMCOS), a new family of finite elements was developed for both linear and non-linear analysis of the Cosserats’ continuum. This significantly facilitated the process of obtaining Cosserat material parameters through a set of experimental tests in which direct measurements were coupled with numerical simulations.

In addition, several experimental studies conducted within FIMCOS demonstrated that the use of classical-elasticity numerical procedures applied to periodic heterogeneous structures—so-called virtual testing—can be highly reliable. The project also produced a number of analytical studies dealing with the high-curvature pure-bending problem in orthotropic classical elasticity and isotropic micropolar elasticity.

Together, these results provide an excellent foundation and a natural starting point for the research conducted in the ANEMIC PM project.

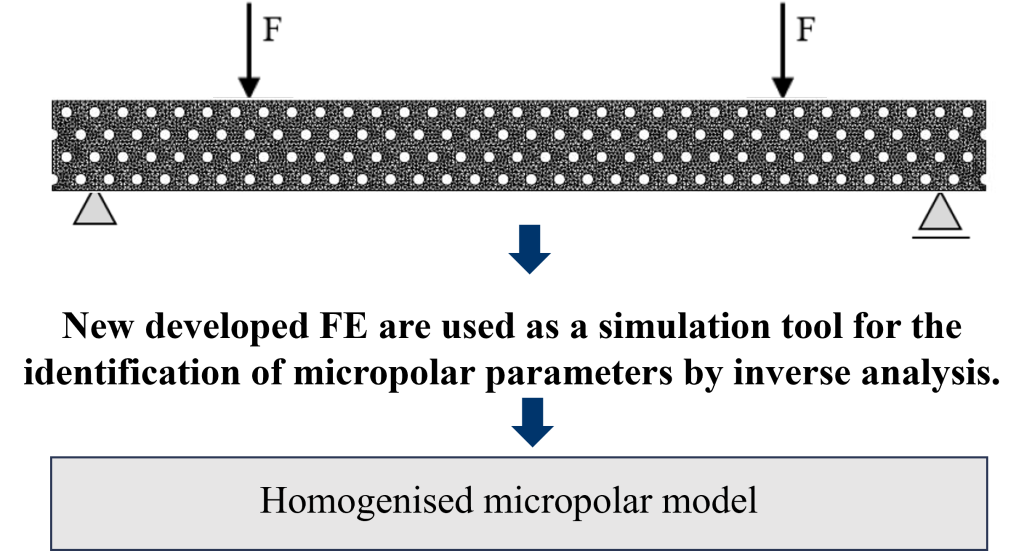
Project summary

In this project, we aim to address several open questions related to the theory, numerical modelling, and experimental testing of Cosserat solids. These questions emerged from the research conducted within the earlier CSF project FIMCOS, and now guide the key directions of the ANEMIC PM project:

1. Can an ‘inverse’ size effect, whereby smaller specimens tend to be softer (and not stiffer) than the larger ones, still be explained by Cosserat’s continuum theory?
2. Can additional analytical solutions for benchmark problems in linear elasticity be derived and made use of for the identification of Cosserats’ material parameters?
3. Can analytical solutions for large-curvature plain-strain pure bending be extended to a wider class of hyperelastic materials (both Cauchy’s and Cosserats’) than currently known, and can they be used to characterise such materials?

In order to answer these questions, the project will carry out a structured set of analytical, numerical, and experimental tasks, summarised in the work-plan highlights below.

Work-plan highlights:

• A set of simple virtual experiments will be conducted on specimens with various relationships between the matrix and the inclusion (O1); the observed behaviour will be catalogued, and the positive or negative size-effect will be explained by eigenanalysis of the whole specimen.
• A couple of benchmark solutions to bending problems will be derived (O2) for assessment of the material parameters obtained under O1; the solutions will be verified numerically.
• Analytical pure-bending solutions will be provided for a new class of hyperelastic materials, which will be used for numerical verification of the procedures to be developed and for parameter identification in the experimental campaign (O3).
• Key project results in O1 and O3 contribute to the theory of Cosserats’ materials’ constitution and address the behaviour of high interest in top-notch emerging technologies.
• Four full-size open-access scientific publications in highly reputable Q1 and Q2 WoS journals are planned; three other submissions are envisaged before the end of the project.
• The national and international events organised annually by the Croatian Society of Mechanics will be regularly attended.
• In addition, four highly reputable international conferences abroad will be visited, including HFSS conference series conceived in Rijeka by our research team.
• The project and its results will be communicated via a dedicated project webpage, Faculty publications, Science Festivals and European Researchers’ Nights in Rijeka.

Research objectives of the project:

• O1 Derive a precise range of values of material parameters in isotropic micropolar elasticity.
• O2 Derive representative analytical solutions for parameter identification.
• O3 Derive pure-bending solution for a wider class of hyperelastic materials.

Expected results:

• Establishing a more accurate and expanded admissible range of Cosserat material parameters, resolving contradictory interpretations reported in earlier studies.
• Derivation of new analytical benchmark solutions for bending problems in linear micropolar elasticity, enabling improved parameter identification.
• Development of analytical pure-bending solutions for a wider class of hyperelastic materials, with extensions from classical to Cosserat hyperelasticity.
• Creation of a new family of nonlinear finite elements for classical and micropolar hyperelasticity, implemented in FEAP and verified against analytical and numerical benchmarks.
• Advanced virtual-testing procedures combining analytical insights and numerical simulations to support robust parameter identification.
• Experimental characterisation of highly deformable hyperelastic specimens, providing data for validation and calibration of nonlinear material models.
• Dissemination of project outputs through high-impact publications, conferences and open-access resources, strengthening the scientific foundation for modelling architected and microstructured materials.

Research team:

Gordan Jelenić, | Google Scholar
Dragan Ribarić, | Google Scholar
Edita Papa Dukić, | Google Scholar
Sara Grbčić Erdelj, | Google Scholar
Laura Grbac, | Google Scholar

Institution:

University of Rijeka, Faculty of Civil Engineering